Soft Body Simulation

RK4, spring coef. 8000, damper coef. 20

Overview

This project simulates a flexible cube falling on the floor, using a framework developed with C++ and OpenGL by GPLab, NCTU. For all the videos of result, please check out the last section.

The cube is constructed by a set of particles, which are connected with 3 kinds of springs. With these particles and springs, we can integrate the spring forces and damper forces to estimate the next positions for each particle. In this case, I implemented Explicit Euler Method and Runge-Kutta 4th-Order Method to solve the differential equations. This is a simple approach to simulate solid deformable objects.

Finally, because it’s a plane there, I also used a simple method to resolve the point-plane collision detection, which can bounce back the cube to the air.

Mass-Spring System

Cube of Particles

As the image above, these particles constructs the cube. In this simulation, it took 1000 particles to form a 10x10x10 cube. Then, the images below shows each kind of the springs connected between particles.

Structural Springs

Structural Springs connect from each particle to its 6 adjacent neighbors, including up, down, left, right, forward, backward. These springs establish the basic structure of the cube.

Shearing Springs

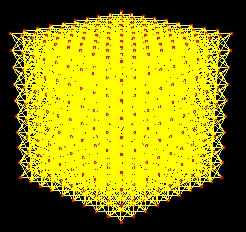
Shearing Springs connect from each particle to its 20 diagonal neighbors. These springs can prevent the cube from excessive shearing.

Bending Springs

Bending Springs connect from each particle to its 6 second adjacent neighbors, kind of like the structural springs but these springs skip the first neighbor instead. They can prevent the cube from folding all over.

Integration

Euler Method

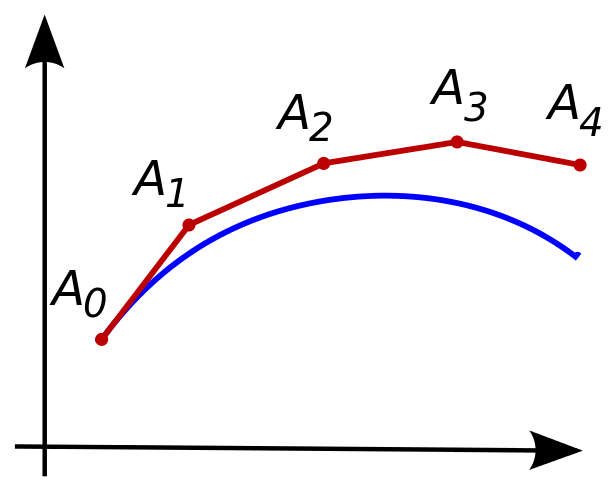
Illustration of the Euler Method (from Wikipedia)

The blue curve in this graph is the unknown real values, while the red one is the approximation by Euler Method. From A0 to A1, this method only takes the status at position A0 to estimate the position after a small time step. In this case, physically, the Euler Method takes the net force at A0 and derive the acceleration to approximate the position at A1 with a small time step.

Because the Euler Method is a first-order method, which means it needs a rather small time step, otherwise the local error (error per step) and the global error (error at a given time) would be very big resulting in unstable system. However, the Euler Method is rather low-cost and also a basic method which is easy to implement.

Runge–Kutta 4th-Order Method

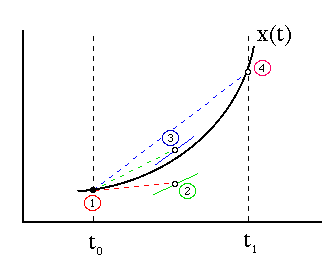
Illustration of the RK4 (from Department of Physics, Drexel University)

First, we define the following equations (h is the step size, h > 0).

• y_n+1 = y_n + (h/6)(k₁ + 2k₂ + 2k₃ + k₄)
• t_n+1 = t_n + h

For k₁, k₂, k₃ and k₄:

• k₁ = f(t_n, y_n)
• k₂ = f(t_n + (h/2), y_n + (h/2)k₁)
• k₃ = f(t_n + (h/2), y_n + (h/2)k₂)
• k₄ = f(t_n + h, y_n + hk₃)

Which means:

• k₁ is the increment based on the slope at the beginning of the interval, using y_n.
• k₂ is the increment based on the slope at the midpoint of the interval, using y_n + (h/2)k₁.
• k₃ is the increment based on the slope at the midpoint of the interval, using y_n + (h/2)k₂.
• k₄ is the increment based on the slope at the end of the interval, using y_n + hk₃.

The RK4 method is a fourth-order method, meaning that it’s rather high-cost and more precise than the Euler Method. It’s local error is on the order of O(h⁵), while the global error is order O(h⁴).

Collision Detection

There is one thing left to handle is the point-plane collision when the cube is falling right on the plane. For every particle, once it satisfies the following conditions, it would be considered that the collision is happening.

• The particle’s position is close enough to the plane.
• The particle is moving toward the plane.

When the particle and the plane are collided, the system would revert the normal component of the velocity. A coefficient smaller than 1 to represent the energy loss could be applied to the reverted velocity. So this is an simple way to handle the point-plane collision.

Results

• Euler Method, spring coef. 8000, damper coef. 20

• Euler Method, spring coef. 800, damper coef. 60

• RK4, spring coef. 8000, damper coef. 20