Fib2584 AI
Overview
Fib2584 is forked from the well-known 2048 with Fibonacci tiles instead of powers of two. It’s developed with JavaScript.
In this Fib2584, I implemented an AI which was trained about 4.3 million games with TD Learning (Temporal Difference Learning). The main concept is training the AI how to evaluate and predict any board’s value to make a suboptimal move. According to the following screenshot of C++ version, which was designed to train this AI, the training result (out of 10000 games) is:
- Win Rate: 85.55% (win - reaching the 610 tile, which is the 14th of Fibonacci)
- Max Score: 64065
- Average Score: 20003
- Max Tile: 4181 (the 18th of Fibonacci)
- 6036.83 moves/sec
Original 2048 is created by Gabriele Cirulli, which is based on 1024 by Veewo Studio and conceptually similar to Threes by Asher Vollmer.
Evaluation
Evaluation is the process to value a certain board. To do this, I defined some features for AI to estimate.
For the following pictures, the left one indicates the 4-tuples outside which has been marked out, and the right one is for the 4-tuples inside. There is a vast difference between outside and inside - for example, the value of a 610 tile at the corner or center are very different. That’s why they can’t be treated the same.
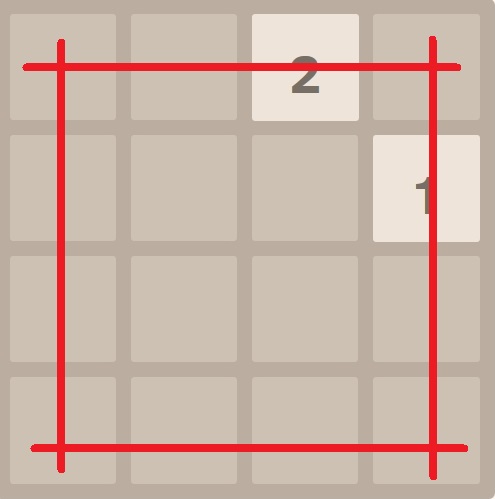
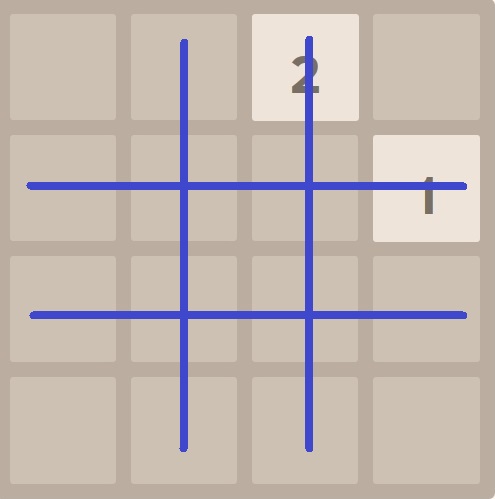
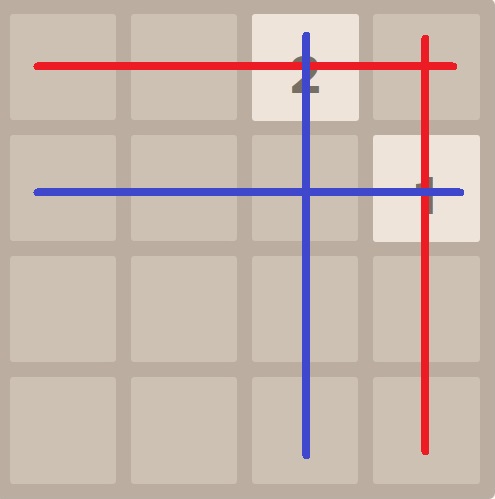
Taking the next picture below for instance, we assume the AI is evaluating this board. First, we evaluate the 4-tuples outside (red). There are 2 non-zero 4-tuples outside, which are [0, 0, 2, 0] and [0, 1, 0, 0] (0 is for empty tile). Then, the non-zero 4-tuples inside are [2, 0, 0, 0] and [0, 0, 0, 1] (blue). And rest of 4-tuples are [0, 0, 0, 0] for both outside and inside. Now we can look up these 4-tuples’ values in trained database (would be explained later) for outside and inside respectively, including the all-zero 4-tuples. Finally, the evaluation would be the sum of the above values.
To pick up the best action to move, the AI would generate the next board for each possible action without new random tile popping out yet, and evaluate these board (may be 4 or less) to compare their values.
Please notice: for the convenience of explanation, here I just ignored the equivalence from symmetry for now. [0, 1, 2, 3] and [3, 2, 1, 0] should be both evaluated and their values would be the same theoretically.
Temporal Difference Learning
To evaluate, we have to train the database by Temporal Difference Learning first.
At the beginning, all values for 4-tuples are initialized as zero. Assuming that there are optimal values for each 4-tuple, the goal would be let AI adjusts itself to these optimal values in the end. Here we used the update function of TD-Afterstate below.
Value(state') ← Value(state') + α[Rewardnext + Value(state'next) - Value(state')]
With Value() indicates the value of a certain state (aka board or position); state is the current board, state’ is the board after performing the best move, and state’next is the board after performing the best move to the next board; Reward is the score got by the moves which could combining some tiles, while Rewardnext is the score got from moving the next board; α is the learning rate less than 1, which sets the adjusting speed of values towards the optimal values.
Only the 4-tuples used would be updated with this function. The Reward is kind of like a critic in this machine learning system, which provided the standard of score in the Fib2584, so the AI could adjust the values depending on it. In addition, the Value(state’next) could be considered as a result of current move; therefore, [Rewardnext + Value(state’next) - Value(state’)] would be the error value to the optimal value. By playing lots of times, the AI would eventually know how to play this game well by itself.


Leave a Comment